医学部受験で最も重視される教科は何でしょうか。

入試の配点をみると、大半の国公立大学では数学と理科が同等で最も大きく、私立大学では理科が全体の半分を占めることもあります。生物や化学は医学に直結する教科で重視されるのもうなずけます。一方で、物理もまた医学に役立つことを東京慈恵会医科大学の2020年度入試問題を例に紹介します。

医学部進学を目指すとき、物理は本当に必要？

医学部入試では、基本的に理科の物理・化学・生物・地学の4科目から2科目を選択する必要があります。しかし、個別試験で地学を選択できるのは東京大学のみで、一般的には残る3科目から選択します。

そのなかで、生物や化学は題材が医学に直結しますが、物理は医学との関連性が薄いように見えます。ところが、生物を必須としている大学はなく、一方で物理を必須とする大学はいくつかあります。

医学部を志望する受験生が物理を学ぶ意義とは何でしょうか。

動脈硬化の予測法を物理で考える

医系単科大学や医学科独自問題を課す大学の中には、この疑問への答えを入試問題として発信しているところがあります。その筆頭が東京慈恵会医科大学です。

例えば、2020年度の入試問題（大問2）には以下のような設問があります。

東京慈恵会医科大学　医学部医学科　2020年度入試問題（改題）

問5（4）このモデルに基づいて考える限りにおいて，血圧の測定で動脈硬化を予測することが可能か不可能かを考察し，その理由を簡潔に説明しなさい。

「これが物理の入試問題なのか？」と不思議に思うような内容です。しかし、これが物理の問題である所以は、冒頭の「このモデルに基づいて考える」という限定条件にあります。

物理とは、自然現象を抽象化し、さまざまな現象に共通する法則性を数学的に解析する手段なのです。その考え方は医学的な題材の解析にも用いることができるのです。

循環器系を電気回路に置き換える

そこで、動脈硬化を解析するためのモデルを、この問題のリード文から見ていきましょう。

血液の粘性（粘り気）は，血管内を流れるときの抵抗になるため，血液を流すには圧力（血圧）をかける必要がある。

管を流れる粘性のある流体について，単純化した模型では，一般に，1秒間に流れる流体の体積（流量）Qは管の両端の圧力差ΔPに比例し，

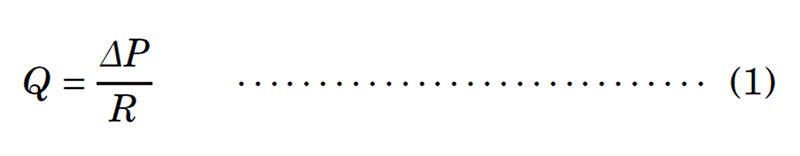
を満たすものとする。ここで，Rは流動抵抗と呼ばれる。（中略）

式（1）において，管の両端の圧力差を電気回路の電位差，流量Qを電流，流動抵抗Rを電気抵抗に対応させると，式（1）は電気回路におけるオームの法則に他ならない。
このように，循環器系で起こる現象を解析するために，循環器系を電気回路に置き換えたもので考えることがよく行われる。置き換えた電気回路を等価回路と呼ぶ。

このように循環器系を電気回路に置き換えて解析していきます。実は、高校物理で電気回路を学ぶときには、この逆の置き換えをしています。電流を水路の水の流れにたとえ、電池は水をくみ上げるポンプとみなすのです。

電気抵抗は水が流れにくい水路や、水の高低差で発電する水車と考えます。また、電気抵抗の並列接続であれば、枝分かれする水路を対応させることで電気回路の法則を学びます。

血管の弾力性や血液の慣性を 電気回路の部品に置き換える

リード文の続きを見ていきましょう。

式（1）においては，血管を太さが変化しない管として扱っている。しかし，実際の血管は血圧が上がると拡張し，血圧が下がると収縮する。（中略）このような現象は，血管の等価回路においてコンデンサーを加えることにより表現できる。

心周期による血流量の時間変化をより正確に表現するには，血液の質量にともなう慣性の影響を取り入れなければならない。慣性は血流量の変化を阻止しようとする力としてはたらくから，等価回路では誘導起電力を発生するコイルで表現できる。

このように血管や血液の性質を電気回路の部品に置き換えて表現し、循環器系全体を一つの電気回路に置き換えます。

心臓から出た血液が全身をめぐって心臓に戻るまでの血管の流動抵抗を抵抗R，血管の弾力性を電気容量C，血液の慣性を自己インダクタンスLで表す。心臓から拍出される時刻tにおける血流量を電流I(t)，血管の両端の圧力差の変動成分を電圧V(t)とすると，図のようなモデルで表すことができる。（後略）

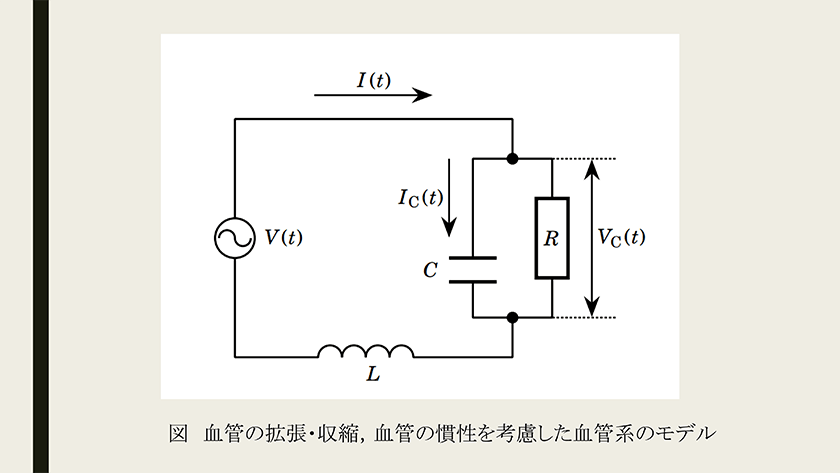
このモデルは高校物理の交流電気回路としては標準的ですが、習っていなくても気にする必要はありません。

大事なことは、血管や血液についてのさまざまな性質をそれぞれ電気回路の部品に置き換える考え方です。血液の粘り気、慣性、血管の拡張・収縮は、言葉で表現すれば全て「流れにくさ」となります。しかし、物理のモデルを用いると、さまざまな「流れにくさ」を区別して表現できるのです。

循環器系のどの性質を測ることが重要かを正確に見抜く

問題は設問部分に入り、電気回路についての考察を経て、以下のように続きます。

問5．血流における慣性の影響が非常に小さな場合を考え，L＝0とする。

（3）　動脈硬化が極度に進行した場合として，血管の弾力性が失われた状態のインピーダンスを求めなさい。

この設問では、循環器系のさまざまな性質のうち、まず血液の慣性の影響が小さく、回路のLが無視できると判断します。設問（3）は血管の弾力性を回路のCにたとえ、動脈硬化が極度に進行した場合にはCが機能しなくなるとして、そのときのV(t) とI(t) との関係（インピーダンス）を考えさせる問題です。

そして、冒頭の設問（4）に続きます。設問（4）の内容を電気回路のモデルで言い換えると、「血圧V(t) を測定して動脈の弾力性Cの変化を予測できるか？」となります。

この設問の解答はいくつか想定できます。まずV(t) の変化の原因としてCの変化だけでなく流動抵抗Rの変化も考えられるので、血液の粘性も測定しないと血圧変化の原因が動脈硬化かどうか分からないとする考え方です。一方で、血液の粘性はあまり変わらないとみなすことができれば、血圧が動脈硬化の指標になると考えることもできます。

どちらが医学的に適した考え方なのかは、この問題の情報だけでは判断できませんが、具体的なCやRの値の大きさや変化幅が分かれば、Cの変化がV(t) の変化にどの程度表れるのかを計算することができます。

つまり、物理のモデルを用いることにより、動脈硬化の進行を判断するための検査項目がわかるのです。

生物や化学の具体的な知識を抽象化して解析するのが物理

もちろん、さまざまな症状を引き起こす動脈硬化、さらに血管の弾力性や血液の粘性・慣性など、モデルに盛り込む具体的な現象の知見は生物や化学の知識に支えられており、医学にとって生物・化学が重要なのは言うまでもありません。一方で、複雑な現象を解析するうえで情報を整理・抽象化する物理の思考法もこのように必ず役に立ちます。

医学部を目指す受験生にとって、高校物理の学習を通して土台となる思考力を鍛えることは重要なポイントの一つです。

また、大学入学後に医学に直結する膨大かつ具体的な知識を学ぶ際や、その後の医師人生においても、あらゆる場面で考え方の一助となるはずです。