代々木ゼミナールでは、京大入試を想定した「京大入試プレ」を年2回、夏と秋に実施しています。ここでは、2015年8月に実施された「第1回 京大入試プレ」受験生の解答例を通して、より高得点に近づくためのアドバイスを記載します。
京大入試数学の特徴は、小問による誘導が少なく、その中で解答者が自分で初期設定をすることや論理的に説明できるかどうかが問われることです。
理系数学
ここでは、「第1回 京大入試プレ」の理系数学において、よく見受けられた誤答例を紹介し、気を付けるべきポイントの解説を行います。ぜひ今後の学習に役立ててください。
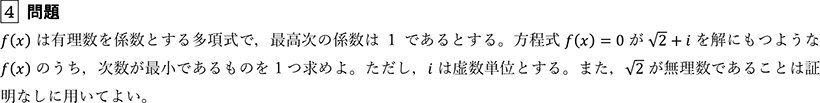
生徒答案例

解説
「条件を満たす多項式のうち次数が最小のものを求めよ」という問題ですから、f(x) が1次式の場合、2次式の場合、…と調べていく方針は立てられたでしょう。
答案例では、2次、3次の場合に係数が有理数のものが存在しないという結論は正しいですが、それぞれ「これを満たす有理数の組はない」根拠となる説明が不足しています。複素数の相等「実数 a、b に対して a+b i=0 ⇔ a=b=0」や「 √2 が無理数であること」によって示すことになります。実際は、余白などで計算をして結論を導いた人もいたでしょうが、答案の中でしっかり説明できていないものが非常に多く見受けられ、減点の対象となりました。
本問では、4次式の場合に条件を満たすものが存在しますが、これが最小の次数であることを示すために、3次以下でないことをしっかり証明することがポイントでした。これを見極め、答案に明示できているか、についてしっかり意識することが必要です。
以上を踏まえて、模範解答を見てみましょう。
模範解答(抜粋)

アドバイス
- 解き方を見定める練習を
-
京大入試において、解き方がすぐに思いつくような典型問題はほとんど出題されません。そのため、必要以上に難しい解き方にはまってしまい、気付いていれば効率よく解けた…ということになりがちです。つまり、初めてみる問題に対する解法の選択が非常に大切になってきます。
普段からいろいろな解法を念頭において演習を行うことが重要です。演習を通じて、問題に応じた最善の解き方を見つける練習を積みましょう。この積み重ねが入試本番にも生かされていきます。
- 書いた答案の見直し
-
解答を書くときには、限られた時間で完璧にすることは難しいものです。ですが、特に計算ミスと論理の間違い・飛躍は大きな減点につながってしまうので、注意が必要です。
普段から、計算を自力で最後まで行う習慣をつけましょう。また、書いた答案に論理的に抜けているところがないか、見直しをする習慣もつけましょう。さらに、自分でよく見直した答案を先生に添削してもらい、自分では発見できないような間違いを指摘してもらうことも有効です。この繰り返しによって、高得点につなげられるようになります。
文系数学
ここでは、「第1回京大入試プレ」の文系数学において、よく見受けられた誤答例を紹介し、気を付けるべきポイントの解説を行います。ぜひ今後の学習に役立ててください。
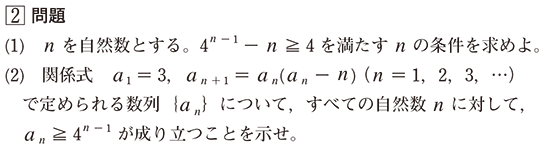
生徒答案例((2)の部分のみ)

解説
本問(2)は、数学的帰納法を用いて不等式を示す問題でした。
上の答案例でも数学的帰納法で示そうとしているのですが、「ここで(1)より、…」の部分に注意して見直してみましょう。
(1)より、不等式(※)が成り立つ条件は k ≧ 3 であり、したがって k ≧ 3 の条件下でのみ a k + 1 ≧ 4k が成り立つことをいっています。よって、上の答案に書かれている意味は( k = 3, 4, 5, …として言い換えると)、
「n = 3 のとき ○ ならば n = 4 のとき ○」、「n = 4 のとき ○ ならば n = 5 のとき○」、…
という関係は成り立つということです。
しかし、前提となる「n = 3 の場合の成立」が示されておらず、この論理の最初で詰まってしまいます。さらに、n = 2 の場合も数学的帰納法の仮定が使えないので示されていないことになります。したがって、n = 2, 3 の場合を示す必要があるというわけです。
このように、数学的帰納法の原理をしっかりと理解しているかを問う問題でしたが、手順は覚えていてもその根本的な理解は不足していると思われる答案が多く見受けられました。
以上を踏まえて、模範解答を見てみましょう。
模範解答((2)の部分のみ)

アドバイス
- 解き方を見定める練習を
-
京大入試において、解き方がすぐに思いつくような典型問題はほとんど出題されません。そのため、必要以上に難しい解き方にはまってしまい、気付いていれば効率よく解けた…ということになりがちです。つまり、初めてみる問題に対する解法の選択が非常に大切になってきます。
普段からいろいろな解法を念頭において演習を行うことが重要です。演習を通じて、問題に応じた最善の解き方を見つける練習を積みましょう。この積み重ねが入試本番にも生かされていきます。
- 書いた答案の見直し
-
解答を書くときには、限られた時間で完璧にすることは難しいものです。ですが、特に計算ミスと論理の間違い・飛躍は大きな減点につながってしまうので、注意が必要です。
普段から、計算を自力で最後まで行う習慣をつけましょう。また、自分の答案の論理的に抜けているところがないか、見直しをする習慣もつけましょう。さらに、自分でよく見直した答案を先生に添削してもらい、自分では発見できないような間違いを指摘してもらうことも有効です。この繰り返しによって、高得点につなげられるようになります。








